小石头 2019-10-24 18:43

上完课回到公司分享，确实有同事说“没有最好只有合适”，我记得您在课上针对这个说了一段话，但周日下午太困，没听明白，翻书也没有又找到。老师能不能告诉我在哪里。

UMLChina潘加宇

书上第一章有一部分：

我再说得详细一些，下次出版时补在书里。
****************************
“没有最好只有合适”这句听起来理中客的话，其实很可能是无知和懒惰的遮羞布。
我用数学类比一下。
妈妈买了苹果和梨共320千克，其中苹果的重量比梨的4倍多20千克，求妈妈买了苹果和梨各多少千克？
没学过未知数、方程等知识的小学生，可能会画线段图：

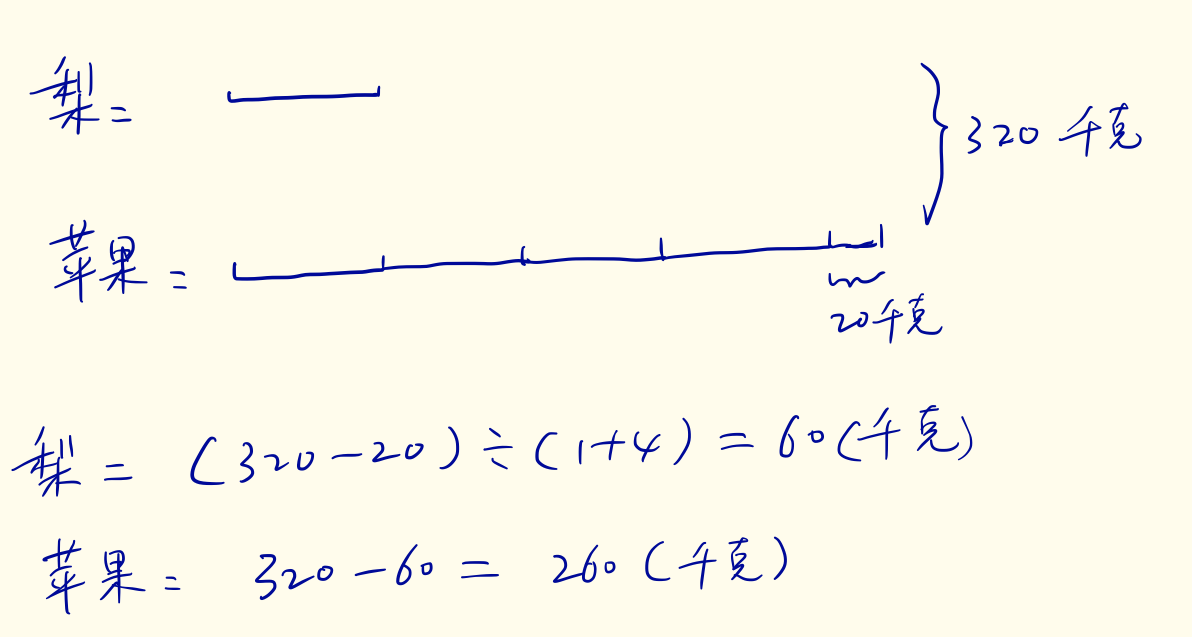
学习了二元一次方程组的初中生，可能用以下方法：

当方程组越来越复杂，初中学习的代入法、消元法已经很难应对。

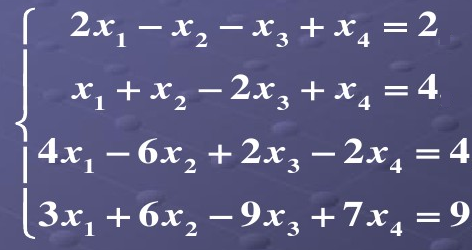
大学的线性代数告诉我们，其实就是矩阵的运算Ax=b，x=b/A，而且还可以用计算机来解（MATLAB）。
上面我们提到了三种知识（1）小学线段图知识（2）初中二元一次方程组知识（3）大学矩阵知识。
下面几点判断应该是合理的：
*学会（2）之后，估计不会再去用（1）了。
*做初中的题来训练脑子玩玩，用（2）更常见。
*复杂的、带来利润的问题，用（3）或更深刻的方法解决更高效，当然，（3）更难，不是所有人都能学会。
下面的想法是天真的：
*只会（1），但以“没有最好只有合适”为由拒绝学习（2）（3）
*老板给你每个月这么高的薪水，是让你解决初中问题玩。
****************************
如果咬牙把书看懂，把将近200道的自测题做对，估计就会清楚，以前自己的做法有多大差距，不会再有“没有最好只有合适”的想法。
遗憾的是，能静下心来学习和思考的人并不多。
****************************
和“没有最好只有合适”类似的遮羞布是By Experience。
如果你探索的是前人没有思考过的问题，说By Experience还有资格。前人已经探索归纳，只是因为自己不知道而且懒得学习，就用By Experience来当遮羞布，脸皮有点厚了。